W świecie informatyki inspiracja przyrodą może prowadzić do fascynujących rozwiązań. Jednym z bardziej ekscytujących przykładów jest zastosowanie algorytmów genetycznych, które czerpią bezpośrednio z mechanizmów ewolucji biologicznej. W środowisku naturalnym ewolucja jest niezwykle skomplikowanym procesem, który pozwala organizmom dostosowywać się do zmieniających się warunków środowiskowych i przetrwać. W informatyce pozwala na rozwiązywanie problemów, które byłyby trudne lub niemożliwe do rozwiązania za pomocą tradycyjnych metod.
Cechą algorytmów genetycznych jest to, że pisząc taki algorytm programista skupia się na opisaniu cech jakie powinno mieć rozwiązanie oraz z czego powinno być złożone, a nie wymyślaniu samego rozwiązania. Zastosowanie losowości (na przykład przy generowaniu kolejnych rozwiązań) wraz z funkcją oceny (jakości znalezionego rozwiązania) prowadzi po pewnym czasie do selekcjonowania rozwiązań, które dostosowują się do funkcji oceny. Podobnie wygląda to w ewolucji biologicznej, w której kolejne osobniki danego gatunku, wraz z upływem czasu i mechanizmom losowości (np. mutacji), coraz lepiej przystosowują się do środowiska, w którym żyją.
Działanie algorytmu genetycznego można przedstawić w następujący sposób:
- losowana jest populacja początkowa, czyli tworzymy (na przykład losowo) jakąś liczbę rozwiązań (osobników) naszego problemu,
- każde z rozwiązań jest oceniane (stosuje się na nich funkcję oceny) oraz sortowane od najlepszego do najgorszego,
- najlepsze rozwiązania biorą udział w procesach krzyżowania oraz mutacji (tworząc nowe rozwiązania),
- nowe rozwiązania zostają ocenione oraz dołączone do populacji,
- z bieżącej populacji wybierane są najlepsze rozwiązania (najlepsze osobniki), które tworzą nową populację.
Kluczowymi w tym algorytmie są następujące elementy:
- genotyp – sposób kodowania rozwiązania osobników. W przypadku kiedy osobnikiem jest rozwiązanie równania 2x + 1 = 0, to genotypem będzie liczba x, na przykład zapisana w formie binarnej.
- funkcja oceny – jest to funkcja, która ocenia danego osobnika. Jeżeli oceniamy rozwiązanie równania 2x + 1 = 0, to funkcja oceny odpowie nam na pytanie, jak bardzo lewa strona równania jest oddalona od zera.
- krzyżowanie – jest to podstawowa operacja w algorytmach genetycznych. Krzyżowanie polega na przepisaniu fragmentów genotypów z dwóch osobników i stworzenie trzeciego. W przypadku równania 2x + 1 = 0, oraz x zapisanego w postaci binarnej będzie to po prostu przepisanie części bitów z genotypu jednego i drugiego osobnika.
- mutacja – kolejna podstawowa operacja w algorytmach genetycznych. Polega ona na losowej zmianie fragmentu genotypu osobnika. W przypadku naszego x będzie to zamiana jednego bitu poszukiwanej liczby.
Przykład prosty
Załóżmy, że mamy następującą funkcję:
oraz nieznane parametry: a, b, c, d, g, które są liczbami całkowitymi z przedziału [-16, 16] (e to liczba Eulera). W jaki sposób możemy dobrać te parametry, aby funkcja przyjmowała następujące wartości:
| X | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
| f(x) | 12.9698 | 17.3094 | 16.1691 | 11.4140 | 5.5832 | 0.9017 | -1.3499 | -1.0008 | 1.2434 |
| X | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 |
| f(x) | 4.2531 | 6.9466 | 8.6238 | 9.0913 | 8.5930 | 7.6187 | 6.6837 | 6.1571 | 6.1815 |
| X | 0.95 | 1.00 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.30 | 1.35 |
| f(x) | 6.6864 | 7.4657 | 8.2788 | 8.9368 | 9.3492 | 9.5277 | 9.5559 | 9.5436 | 9.5854 |
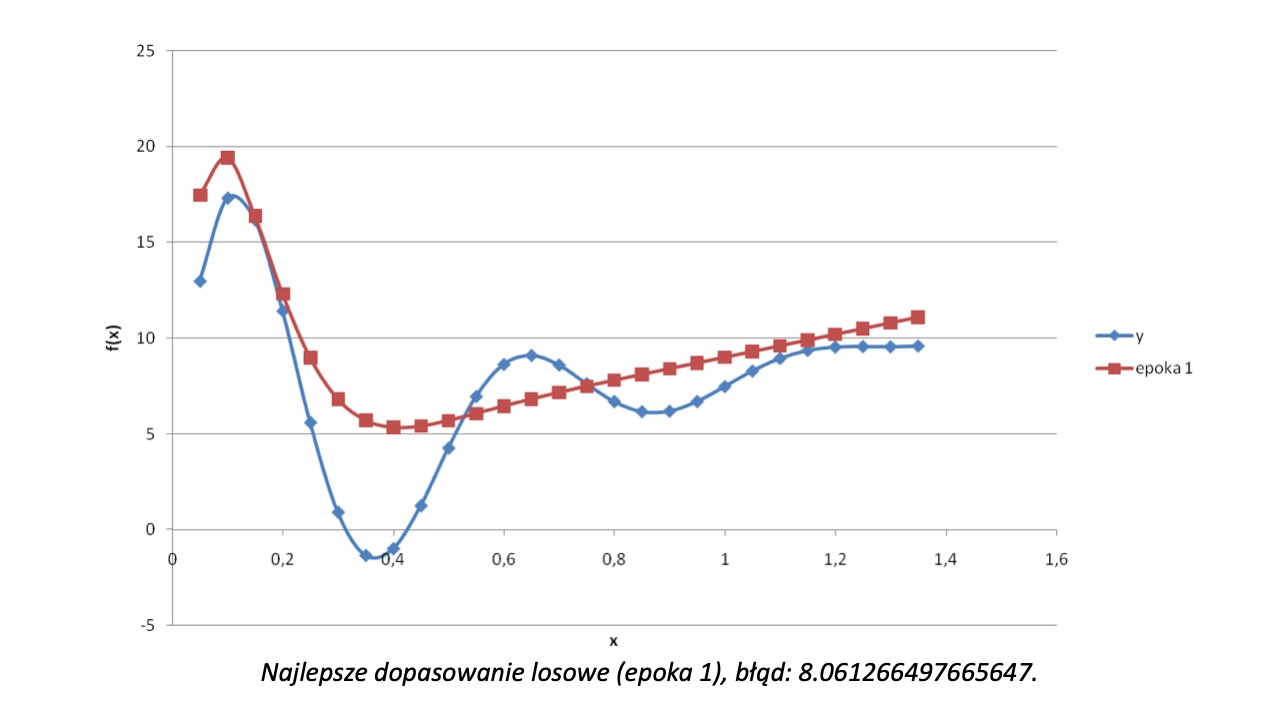
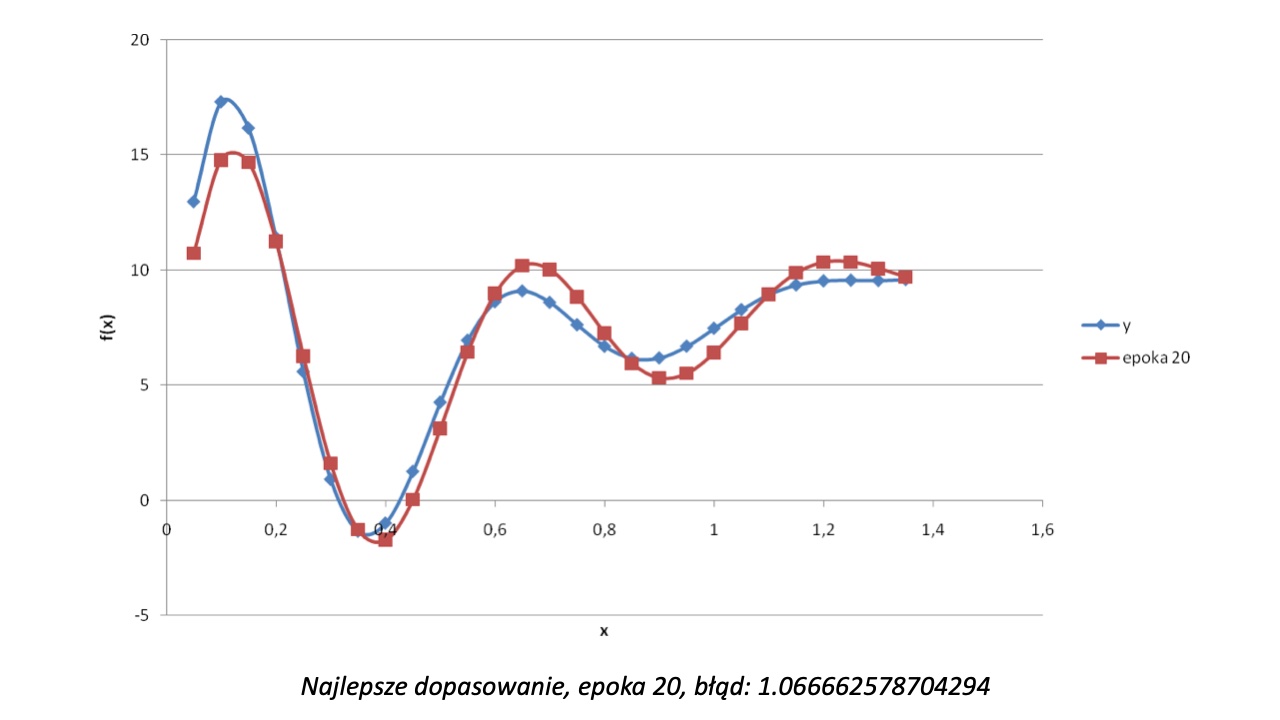
Na pierwszy rzut oka ten problem może wydawać się nie do rozwiązania. Możemy zgadywać jakie są wartości parametrów, ale przy skomplikowanych funkcjach ta metoda nie będzie skuteczna z powodu zbyt wielu zależności między parametrami. Możemy też spróbować przetestować wszystkie dostępne wartości, ale to podejście jest nieefektywne obliczeniowo. Przy jednym parametrze całkowitym mamy do dyspozycji 32 wartości, przy dwóch parametrach jest to już 32 * 32 = 1024 wartości. Z pomocą przychodzi nam wiedza na temat algorytmów genetycznych.
W rozwiązaniu takiego problemu genem osobnika jest tablica zawierająca w sobie pięć liczb, która ulega operacjom krzyżowania i mutacji (operacje bitowe) w zależności od pewnych przyjętych na początku parametrów (szansy zajścia tych operacji). Kluczowym elementem algorytmu jest określenie funkcji celu (określającej stopień dopasowania osobnika do szukanej funkcji). Do tego możemy wykorzystać błąd średniokwadratowy. Dodatkowo ustalamy warunek wyjścia (czyli kiedy uznajemy, że osiągnięty wynik nas zadowala). Tak przygotowany algorytm genetyczny generuje następujące wyniki:
Przykład widowiskowy
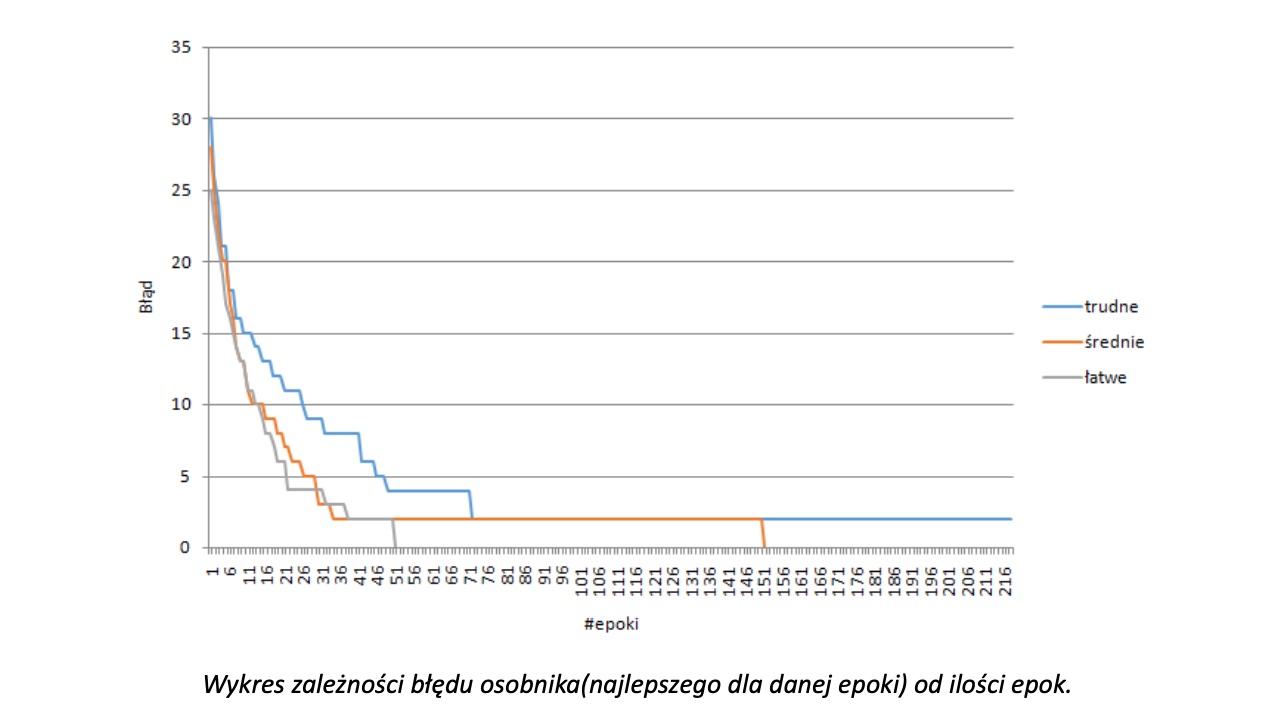
Rozważmy inny przykład i spróbujmy wykorzystać algorytmy genetyczne do rozwiązywania plansz sudoku. Sudoku to gra, której celem jest uzupełnienie planszy 9×9 tak, aby w każdym rzędzie, każdej kolumnie oraz każdym bloku 3×3 była tylko jedna z cyfr (1-9).
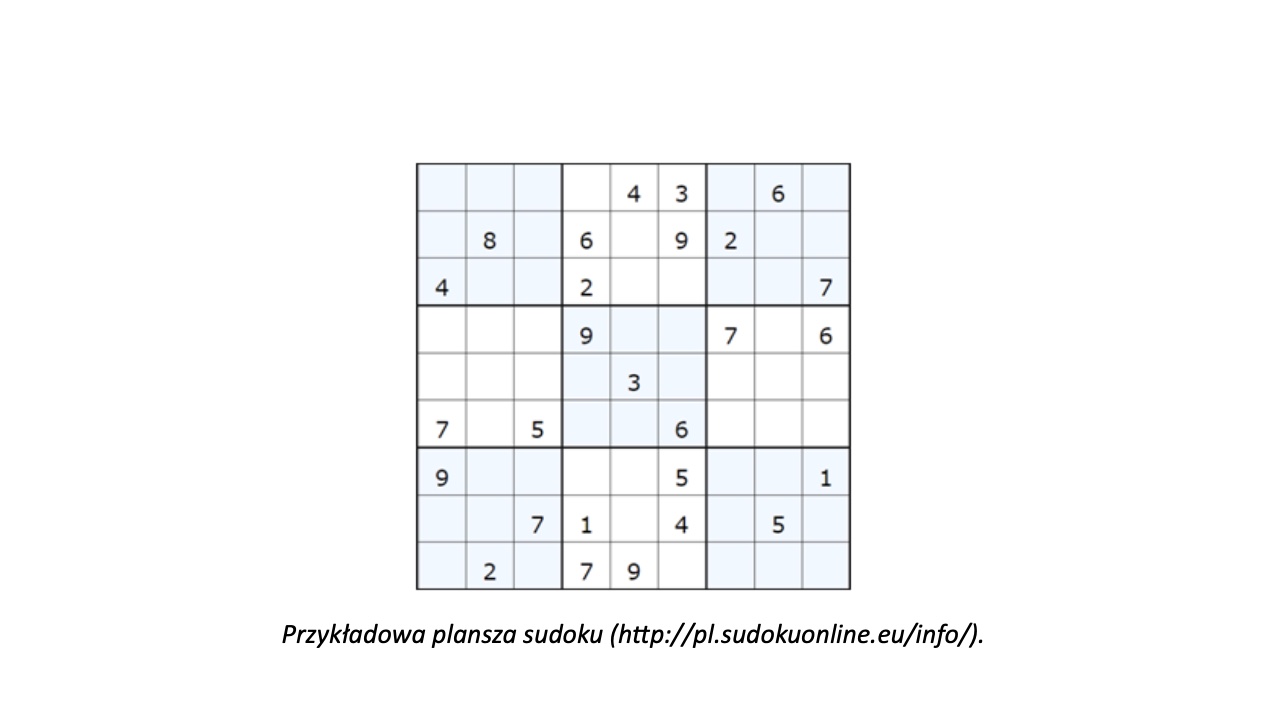
Plansze sudoku można podzielić ze względu na poziom trudności. Te proste są wypełnione w około 35% i nie zawierają niejednoznaczności. Te najtrudniejsze są wypełnione w około 20% i nie można jednoznacznie ustalić konkretnych pozycji cyfr (na planszy jest dużo cyfr które występują tylko jeden raz, więc nie można ustalić jednoznacznie pozostałych miejsc).
W tym przypadku naszym genomem będzie plansza wypełniona w sposób losowy, jednak z zastosowaniem jednej reguły: bloki 3×3 wypełnione są w taki sposób, że cyfry w nich nie mogą się powtarzać. Reguła mówiąca o tym, że cyfry we wszystkich wierszach i kolumnach nie mogą się powtarzać może zostać pominięta.
Określmy też, w jaki sposób oceniamy tak przygotowaną planszę sudoku. Możemy uznać, że jeżeli:
- w bloku 3×3 występują powtórzenia, to za każde z nich osobnik otrzymuje +1 punkt karny,
- w kolumnie występują powtórzenia, to za każde z nich osobnik otrzymuje +1 punkt karny,
- w wierszu występują powtórzenia, to za każde z nich osobnik otrzymuje +1 punkt karny.
Krzyżowaniem będzie wzięcie jednej części planszy z jednego osobnika i dobraniem brakującej części z innego. Krzyżowanie odbywa się między osobnikami w sposób losowy, czyli mamy jakąś określoną szansę na to, że nastąpi operacja krzyżowania na dwóch osobnikach. Również sposób krzyżowania (czyli określenia, jaka część planszy jest wzięta z jednego osobnika, a jaka z drugiego) jest określona w sposób losowy.
Mutacją będzie operacja zamiany dwóch cyfr wewnątrz jednego bloku 3×3. Wybór bloku oraz pary cyfr następuje w sposób losowy. Tak przygotowany algorytm może rozwiązać sudoku łatwe i średnie. Nie radzi sobie natomiast z planszami o podwyższonej trudności – bardzo często wpada w minimum lokalne. Można to porównać do sytuacji, w której kończymy rozwiązywać sudoku i okazuje się, że ostatnia wpisana cyfra nie pasuje).
Przykład prawdziwy
Ewaluacja to ocena jakości działalności naukowej, którą przeprowadza się cyklicznie w ramach dyscyplin naukowych w ocenianym podmiocie naukowym przez Ministerstwo Edukacji i Nauki. Efektem ewaluacji jest przyznanie dyscyplinom w podmiocie kategorii naukowych A+, A, B+, B, C. Przy dokonywaniu oceny brane są pod uwagę osiągnięcia pracowników: publikacje w formie artykułów naukowych, rozdziałów w monografiach, całych monografii, wykazywane w poszczególnych dyscyplinach, które mają pewną wartość wyrażoną w punktach. Sam proces ma kilka ograniczeń, między innymi:
- limity na ilość osiągnięć danego pracownika w ramach dyscypliny naukowej,
- limit na ilość osiągnięć w ramach instytucji, w stosunku do której przeprowadzana jest ewaluacja.
Celem jest takie dobranie tych osiągnięć, aby nie przekroczyć zadanych limitów oraz zmaksymalizować wartość osiągnięć dla ewaluowanej instytucji w ramach dyscypliny naukowej. Aby wyznaczyć maksymalną wartość dla tak postawionego zadania, należałoby sprawdzić każdą możliwą kombinację osiągnięć aż do uzyskania maksymalnego wyniku. Problemem jest to, że aby sprawdzić na przykład 32 osiągnięć, należałoby porównać 2^32 różnych kombinacji (każde z osiągnięć możemy wziąć do ostatecznego wyniku lub odrzucić).
Z takim problemem spotkało się Laboratorium Inżynierii Lingwistycznej, w ramach którego zrealizowano system SEDN (System Ewaluacji Dorobku Naukowego). Kluczowym elementem tego systemu był algorytm genetyczny, który pozwolił na rozwiązanie tego zadania. W tym przypadku genomem był wektor składający się z zer i jedynek (osiągnięcie jest brane pod uwagę albo nie), który wpływał na ocenę danego osobnika, a funkcja określająca jakość osobnika odrzucała rozwiązania, które przekraczały limity. Wypracowany algorytm zawierał mnóstwo usprawnień i optymalizacji pozwalających szybciej osiągnąć wyniki, jednak opierał się na tych samych prostych zasadach opisanych w przykładach powyżej. Dla 1097 przeprowadzonych ocen tylko w dwóch przypadkach udało się polepszyć wynik.
Należy również pamiętać, że algorytmy genetyczne nie są rozwiązaniem na wszystkie problemy. Jak pokazano na przykładzie sudoku, potrafią bardzo długo i nieskutecznie szukać rozwiązania, wpadać w lokalne minimum. Sam algorytm nie gwarantuje znalezienia najlepszego rozwiązania, tylko rozwiązanie spełniające założone przez nas kryteria.